Intro 2 Isogeny
:: Contents
TL:DR
一些关于 SIDH、CSIDH 的直观理解,以及此前出过或遇见的偏简单适合入手的同源题目。
今年暑假 Crypto Hack 更新了一些与 Isogeny 相关的东西,比较推荐上手做一做,适合入门。
Isogeny
Background
曲线同源不同于传统密码学中曲线离散对数(ECDLP)的内容,在此前我们更多地研究已知等式 $[a]P=Q$ 中的 $P,Q$ 要求找到 $[a]$。这相当于是考虑点之间的关系,但在曲线同源中研究的是曲线之间的关系。由于量子计算机以及 Shor 算法的产生,后量子密码学得到了很多的关注,基于曲线同源的密码学就是其中一种,在此前Nist后量子的候选中还有一些其他的诸如基于格,基于编码,基于多变量,基于哈希函数,基于MPC的密码体系等等。相比其他体系基于曲线同源的密码学优势在于其密钥短,但缺点是计算速度较慢。
Curve Isogeny(曲线同源,下简记为同源)是什么?🤔
同源其实就是一种态射,或者说是一个有理函数。对于曲线 $E_1,E_2$ ,映射 $\phi:E_1\rightarrow E_2$ 满足对于任意两点 $P,Q\in E_1$ 有 $\phi(P+Q)=\phi(P)+\phi(Q)$ ,并且 $\phi(O_{E_1})=O_{E_2}$ ,我们称这样的函数 $\phi$ 为曲线 $E_1$ 到 $E_2$ 的同源。
对于一个态射我们经常会考虑它的原像、像以及核($Ker(\phi)=\set{X|\phi(X)=O}$)。在与同源相关的密码系统中通常做的最多的有两种操作,在给出曲线和核的情况下计算同源,在已知同源的情况下评估原像上点在像上对应的点。
实际上除了有关曲线的同源还有各种奇怪数学结构的同源问题,像编码同源或者多变量同源等,就看怎么定义映射了。
在 SageMath 通过原像及对应的核定义同源 $\phi$
sage: ells = [*primes(3, 250), 661]
sage: p = 4 * prod(ells) - 1
sage: F = GF(p, 'i')
sage: A = 0
sage: E = EllipticCurve(F, [0, A, 0, 1, 0])
sage: while not (P := (p + 1) // 3 * E.random_element()): pass
sage: φ = E.isogeny(P)
核和映射之间满足的关系
sage: P.order() == φ.degree()
实际上,之前的表述并不严谨,核很明显应该为一集合,但这里只是将 $P$ 作为了参数,实际上这代表了这样一个集合 $\set{k\cdot P|k\in \mathbb{Z}}$,更简洁的可以把这记为 n-torsion (其中 $n$ 为 $P$ 的阶)。通过实验,可以发现同源的度数和核的势相等,当然应该有更严谨的说法,限于水平只能通过类似实验的方式去验证同源的大多数性质了。
基于同源的困难问题是什么?😖
这大概是入手同源时最费解的一个问题了,不同于此前接触过的基于大整数分解、离散对数、格上短向量问题,同源的困难性理解起来有点抽象。简单来讲就是给定原像 $E$ 和像 $E’$ 找到它们间的映射 $\phi$ 是困难的,当然这个困难程度和我们选择的参数有关系,对于小规模参数下的问题我们只需要枚举所有可能情况即可求解。这里给出一些直觉上的理解,同源相关的困难问题往往可以视为在一个节点数特别多的复杂图结构中找到两点之间的路径,后面会提到的 SIDH 就是 2-isogeny graph, 3-isogeny graph,而 CSIDH 则是相对更工整一点的图。


Basics
具体介绍同源相关的密码学协议前先补充一部分必要的曲线🧀。
Supersingular Elliptic Curve
记 $q=p^k$,当满足 $\verb|#|E(F_q)\equiv1(mod\ p)$ 时我们称曲线 $E$ 为超奇异椭圆曲线。
实际上对于超奇异椭圆曲线的定义有非常多种,有一种比较有趣的 End(E) is an order in a quaternion algebra,这个定义方式可能对于理解后面 SIDH 是有益的。
超奇异曲线上的 ECDLP 是脆弱的,MOV attack 可以计算低嵌入度曲线上的 ECDLP。但是在同源中采用超奇异曲线在保证安全性的同时会带来更快的计算速度。
sage: E.is_supersingular()
j-invariant
用来判断两曲线是否具有同构关系的量,若两曲线的 j-invariant 相等则两曲线在当前域或其扩张上存在同构关系。
曲线 $E:\ y=x^3+Ax+B$ 的 j-invariant 可表示为 $j(E)=j(A,B)=1728\frac{4A^3}{4A^3+27B^2}$
sage: E.j_invariant()
Montgomery model
形如 $E:\ y^2=x^3+Ax^2+x$ 的曲线,这种形式在 CSIDH 的 action group 构造上会用到。实际上这里的 $A$ 也可以视为一种不变量,在 $F_p$ 上的超奇异曲线由于 j-invariant 不足以区分曲线 $E$ 和它的二次扭转 $E’$ ,所以 CSIDH 会选择用 $A$ 来作为一种标识曲线的方法。而 SIDH 在 $F_{p^2}$ 上 ,由于引入了 $i$ ,j-invariant 能作为曲线的标识。
sage: E.montgomery_model()
Pairing
令 $G_1,G_2,G_t$ 为相同阶的循环群,记 $e:G_1\times G_2\rightarrow G_t$ 是从直积群 $G_1\times G_2$ 到 $G_t$ 的映射,当满足下述性质时称其为双线性映射。
- 对于 $\forall\ U,V\in G_1,\ W\in G_2$ ,$e(U+V,W)=e(U,W)\cdot e(V,W)$
- 对于 $\forall\ U\in G_1,\ V,W\in G_2,\ e(U,V+W)=e(U,V)\cdot e(U,W)$
- 对于 $\forall\ P\in G_1,P\ne O$ 存在 $Q\in G_2$ 使得 $e(P,Q)\ne1$ ,对于 $Q\in G_2$ 类似
常见的 Weil pairing 和 Tate pairing 都是椭圆曲线加法群到有限域乘法群的映射,即 $G_1=G_2=E$ ,$G_t=F_q$
SIDH
SIDH (Supersingular Isogeny Diffie-Hellman) 的几个关键元素:同源、超奇异、DH。
这是一种基于同源的在超奇异曲线上类似DHKE的密码学协议。
在得到完整的SIDH协议前我们需要为 Alice 和 Bob 做一些准备,
Alice:起始曲线 $E$,$E[2^a]$ 上的 torsion basis $P_A,Q_A$,私钥 $sk_a$
Bob:起始曲线 $E$,$E[3^b]$ 上的 torsion basis $P_B,Q_B$,私钥 $sk_b$
为了保证存在 $2^a,3^b$ 为阶的点,在 SIDH 中将曲线所在域设置为 $F_{p^2}$ 其中 $p=2^a3^b-1$
在这个设置下超奇异曲线 $E$ 的阶为 $(p+1)^2$,那么上述的 torsion basis 都是存在的。而选择 $2^a,3^b$ 这样的结构是因为这样算的比较快,若是对于一般的 $t|p+1$,在 t 较大时通过 Vélu 公式 $O(t)$ 或者 √élu $O(\sqrt{t})$ 计算 t-isogeny 是非常慢的。但是小素数的幂这种结构能通过复合的方式进行,比如 $2^a$-isogeny 只需要 a 次 2-isogeny 就要快很多。
SIDH 面临的主要技术难点是超奇异曲线的自同态环非交换,结合上面所说的超奇异曲线的定义,实际上就是说 $F_{p^2}$ 上的曲线自同态环同构于四元代数的某个整环,但这个整环对乘法是一个非交换的结构,而 D-H 类型的协议需要交换性。
sage: p = 2**12 * 3**13 - 1
sage: Bpinf = QuaternionAlgebra(p)
sage: α = Bpinf.random_element()
sage: β = Bpinf.random_element()
sage: assert α*β != β*α
为了解决这个问题,SIDH在协议中引入了额外辅助点,来帮助双方最后得到一致的共享密钥。这使得SIDH并不是基于纯粹的 isogeny path problem 了,也是后面 SIDH 被攻破的原因。
Protocol
Setup:
- $p=l_A^{e_A}l_B^{e_B}\cdot f-1$,固定 $F_{p^2}$ 上的超奇异曲线 $E$
- Torsion bases $\set{P_a,Q_a}\in E[l_A^{e_A}]$ ,$\set{P_b,Q_b}\in E[l_B^{e_B}]$
sage: a, b = 216, 137
sage: p = 2**a*3**b-1
sage: F.<i> = GF(p**2, modulus=x**2+1)
sage: E = EllipticCurve(F, [1, 0])
sage: while True:
....: Pa, Qa = [E.random_point()*3**b for _ in range(2)]
....: if Pa.order() == Qa.order() == 2**a and Pa.weil_pairing(Qa, 2**a).mult
....: iplicative_order() == 2**a:
....: break
sage: while True:
....: Pb, Qb = [E.random_point()*2**a for _ in range(2)]
....: if Pb.order() == Qb.order() == 3**b and Pb.weil_pairing(Qb, 3**b).mult
....: iplicative_order() == 3**b:
....: break
Key Exchange:
- Alice 选择随机 $sk_a\in[0,l_A^{e_A}-1]$,Bob 选择随机 $sk_b \in [0,l_B^{e_B}-1]$,Alice 将 $R=P_a+sk_a*Q_a$ 作为 Kernel 计算 $\phi_a:E\rightarrow E_a$,Bob类似通过 $S$ 计算出 $\phi_b:E\rightarrow E_b$
sage: ska = randint(0, 2**a-1)
sage: skb = randint(0, 3**b-1)
sage: R = Pa+ska*Qa
sage: S = Pb+skb*Qb
sage: φa = E.isogeny(R, algorithm="factored")
sage: φb = E.isogeny(S, algorithm="factored")
- Alice 计算 $\phi_a(P_b),\phi_a(Q_b)$ 并发送给 Bob,Bob 类似操作。
sage: Ea = φa.codomain()
sage: Pba, Qba = φa(Pb), φa(Qb)
sage: Eb = φb.codomain()
sage: Pab, Qab = φb(Pa), φb(Qa)
- Alice 将 $R’=\phi_b(R)=\phi_b(P_a)+sk_a*\phi_b(Q_a)$ 作为 Kernel 计算 $\phi_{ba}:E\rightarrow E_{ba}$,Bob同理。最后由于 $E_{ab}\cong E_{ba}$,考虑 j-invariant 最终能协商到一致的密钥 $j(E_{ab})=j(E_{ba})$
sage: Rb = Pab+ska*Qab
sage: jba = Eb.isogeny(Rb, algorithm="factored").codomain().j_invariant()
sage: Sa = Pba+skb*Qba
sage: jab = Ea.isogeny(Sa, algorithm="factored").codomain().j_invariant()
sage: assert jab == jba
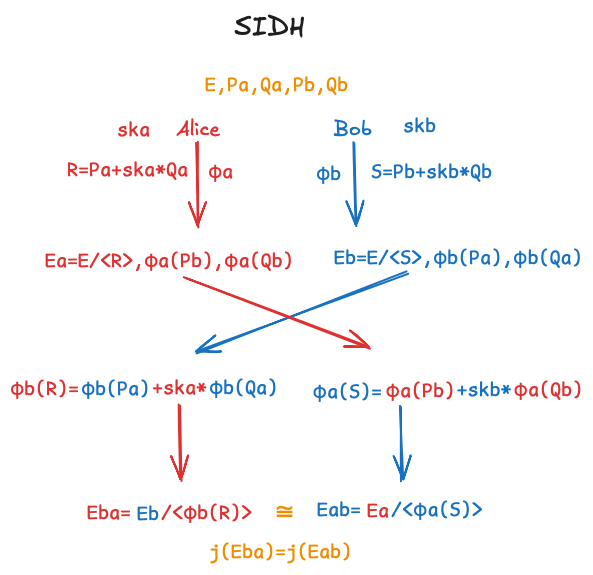
图示如下:
Security
SIDH 基于的安全性可以转换为下面的命题
SupperSingular Computational Diffie-Hellman Problem(SSCDH):给定曲线 $E_a,E_b$ 以及一些点 $\phi_a(P_b),\phi_a(Q_b),\phi_b(P_a),\phi_b(Q_a)$ ,计算 $E/\langle P_a+[sk_a]Q_a,P_b+[sk_b]Q_b\rangle$ 的 j-invariant。
Isogeny Path Problem:给定曲线 $E,E’$,计算 $E$ 到 $E’$ 之间的映射。
实际上将 SSCDH 换成下面这种表述方案只是给出了额外的 $E,E’$ 间映射的两组像原像对。
结论就是这样非常不安全,从之前的一系列 torsion point attack 到现在 key recover attack 都是利用了所给的辅助点信息。
Castryck-Decru Key Recovery Attack on SIDH Repo
CSIDH
CSIDH 中的 C 指的是 Commutative,不同于 SIDH 需要引入辅助点,这里的结构本身就是交换的。🏝️
首先需要先建立几个会频繁出现的数学名词直觉,
$End(E)$: $E$ 对应的自同态环,也就是原像和像都是 $E$ 的同态映射的一个集合
$\mathcal{O}$ (Order): 可以简单理解为代数数域上的子环,类似高斯整环 $\mathbb{Z}[\sqrt{-1}]$ 这种就可以叫 Order
$\mathcal{Ell}(\mathcal{O},\pi)$: 所有自同态环与 $\mathcal{O}$ 同构的曲线类,$\pi$ 指 Frobenius 映射
$cl(\mathcal{O})$:理想类群,i.e. $\mathcal{O}$ 中理想集商去等价关系,直观上感觉是对 $\mathcal{O}$ 做了一个分类
$[\mathfrak{l}]\in cl(\mathcal{O})$: 理想类,包含了一些理想,这些理想作用在 $\mathcal{Ell}(\mathcal{O},\pi)$ 中的曲线后像同构
下面来看 CSIDH 中最重要的操作 group action
定义:$\mathcal{O}$ 是虚二次域上的一个整环,且 $\pi\in\mathcal{O}$,$\mathcal{Ell}_p(\mathcal{O},\pi)$ 非空。那么理想类群 $cl(\mathcal{O})$ 作用在 $\mathcal{Ell}_p(\mathcal{O},\pi)$ 上自由可迁,其作用过程可表述为 $$ cl(\mathcal{O})\times \mathcal{Ell}_p(\mathcal{O},\pi)\rightarrow \mathcal{Ell}_p(\mathcal{O},\pi):\ ([\mathfrak{a}],E)\mapsto E/[\mathfrak{a}] $$ 那这个过程是怎么和同源关联起来的呢,下面更直观地理解 $([\mathfrak{a}],E)$ 的过程,一层层来翻译,考虑 $\mathfrak{a}$ 对 $E$ 的作用,因为 $\mathfrak{a}$ 是 $\mathcal{O}$ 的理想,而 $\mathcal{O}$ 同构于 $\mathcal{Ell}$ 中元素的自同态环,所以 $\mathfrak{a}$ 也可以看成自同态环的理想,其中包含了一些自同态映射,取其中每个自同态映射核的交能得到一些点的集合记为 $\widetilde{\mathfrak{a}}$,而 $E/[\mathfrak{a}]$ 也就是 $E/\widetilde{\mathfrak{a}}$ 。
那么这种观点下就比较方便理解 CSIDH 的交换性了,CSIDH的交换性和理想类群的交换性直接挂钩,只需要说明 $[\mathfrak{a}][\mathfrak{b}]=[\mathfrak{b}][\mathfrak{a}]$,也就是 $\mathcal{O}$ 上元素是否具有交换性,对于 CSIDH 只要验证对应的 $\mathbb{Z}[\pi]$ 也就是 $\mathbb{Z}[\sqrt{-p}]$ 就行。
sage: ells = [*primes(3, 250), 661]
sage: p = 4 * prod(ells) - 1
sage: K.<i> = NumberField(x^2+p)
sage: O = K.order([1, i])
sage: α = O.random_element()
sage: β = O.random_element()
sage: assert α*β == β*α
这样理解的话,CSIDH 的结构和常见的 Dlog 的结构是可以联想起来的,因为都是交换的结构,但是由于 Shor 算法的出现 Dlog 可以在多项式时间求解,但是对于 CSIDH 只能算是 Hidden shift problem,对其最好的攻击是 Kuperberg 的亚指数时间攻击。
Protocol
Setup:
- 选择 $p=4\cdot l_1l_2\dots l_k-1$ ,其中 $l_i$ 为小奇素数,设置一个 $F_p$ 上起始超奇异曲线 $E:y^2=x^3+x$,自同态环为 $\mathbb{Z}[\sqrt{-p}]$
sage: ells = [*primes(3, 250), 661]
sage: p = 4 * prod(ells) - 1
sage: F = GF(p, 'i')
- Alice 选择私钥 $[\mathfrak{a}]$ ,Bob 选择私钥 $[\mathfrak{b}]$ ,由上面提到的 $[\mathfrak{a}]$ 与同源计算的关系,实际上 $[\mathfrak{a}]$ 可以看成做哪些 $l_i$-isogeny 。
sage: priv1 = [randint(-3, 3) for _ in range(len(ells))]
sage: priv2 = [randint(-3, 3) for _ in range(len(ells))]
Key Exchange
sage: def csidh(A, priv):
....: E = EllipticCurve(F, [0, A, 0, 1, 0])
....: for sgn in [1, -1]:
....: for e, ell in zip(priv, ells):
....: for i in range(sgn * e):
....: while not (P := (p + 1) // ell * E.random_element()):
....: pass
....: P.set_order(ell)
....: E = E.isogeny_codomain(P)
....: E = E.quadratic_twist()
....: return E.montgomery_model().a2()
- 分别计算 $E_a=[\mathfrak{a}]\star E,E_b=[\mathfrak{b}]\star E$
sage: Ea = csidh(0, priv1)
sage: Eb = csidh(0, priv2)
- 双方根据对方传来的 $E_b$ 或 $E_a$ 计算 $E_{ba},E_{ab}$ ,协商出一致的密钥 $A(E_{ba})=A(E_{ab})$
sage: assert csidh(Ea, priv2) == csidh(Eb, priv1)
图示如下:

Security
CSIDH 的安全性由 CSSCDH 的强度决定
CSSCDH:记 $p,E$ 均为 CSIDH 中的参数,给出 $E,[\mathfrak{a}]\star E,[\mathfrak{b}]\star E$ 计算 $[\mathfrak{a}]\star [\mathfrak{b}]\star E$ 是困难的,其中 $\mathfrak{a},\mathfrak{b}$ 为 $\mathcal{O}$ 中的随机元素。
由于 CSIDH 与 SIDH 不同,不需要辅助点的介入,这也使得其可以免疫大多针对 SIDH 的基于给出扭转点像的攻击。
Challenges
| CTF | Challenge | Difficulty | Overview |
|---|---|---|---|
| N1junior 2024 | IEV@L | ⭐ | 中间相遇,外加一点简单pyjail |
| M0leconCTF 2022 | SIDHalf | ⭐ | Weil pairing在同源下的应用 |
| DiceCTF 2023 | seaside | ⭐ | CSIDH 二次扭转 |
| jqctf-quals 2024 | BabyOracle2 | ⭐⭐ | GPST Attack |
| RCTF 2022 | S2DH | ⭐⭐ | Castryck-Decru Attack,有现成的repo。需要根据论文内容修改起始曲线的自同态环求法。 |
| jqctf-quals 2024 | S2DH+ | ⭐⭐⭐ | 起始曲线有已知的自同态环,参考 Petit’s Attack 大致思路 |
Reference
[1] CSIDH: An Efficient Post-Quantum Commutative Group Action ↩
[2] Supersingular isogeny key exchange for beginners ↩
[3] Mathematics of Isogeny Based Cryptography ↩
[4] CSIDH方案短课(沙龙)↩
[5] Divisors and Pairings ↩